Отбор корней в тригонометрических уравнениях
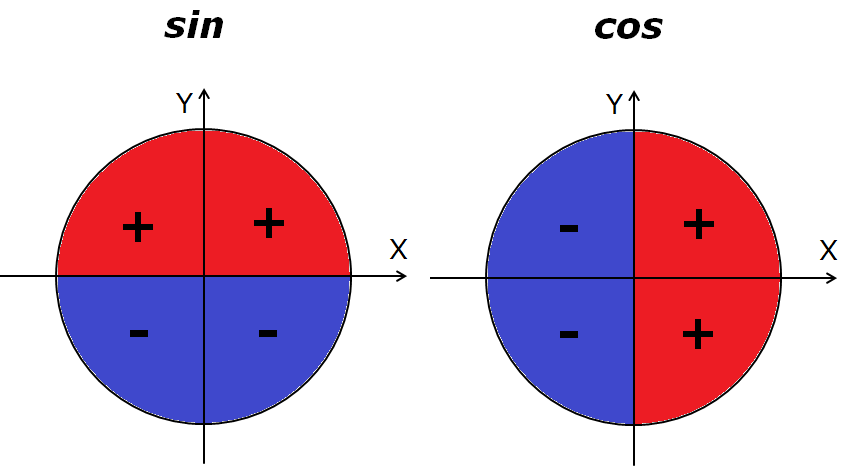
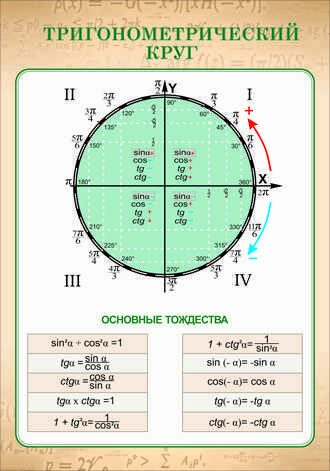
Многие выражения, содержащие синусы и косинусы становятся значительно проще, если пользоваться надежным инструментом — тригонометрическим кругом. А для этого нужно три простых шага и запомнить их: один раз сделал, запомнил и заслуженная пара баллов в кармане. Синус положительный в первой и второй, косинус в первой и четвертой, а тангенс и котангенс одинаково положительны в первой и третьей. На картинке указаны знаки тригонометрических функций, которые смело можно сохранять.
.jpg "Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике")
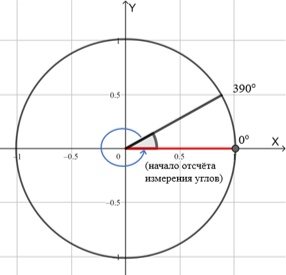
Если проще: это уравнения, в которых неизвестные иксы или выражения с ними находятся внутри синусов , косинусов , тангенсов и котангенсов. Такие тригонометрические уравнения называются простейшими. Их легко решать с помощью числовой окружности тригонометрического круга или специальных формул:.
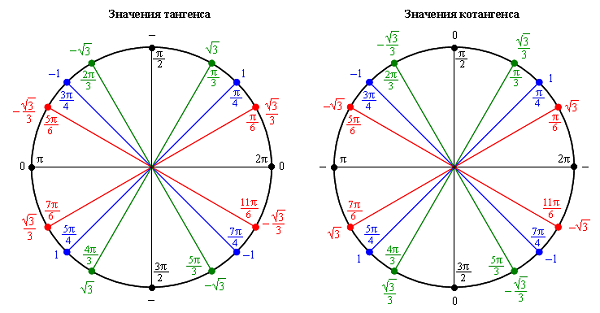
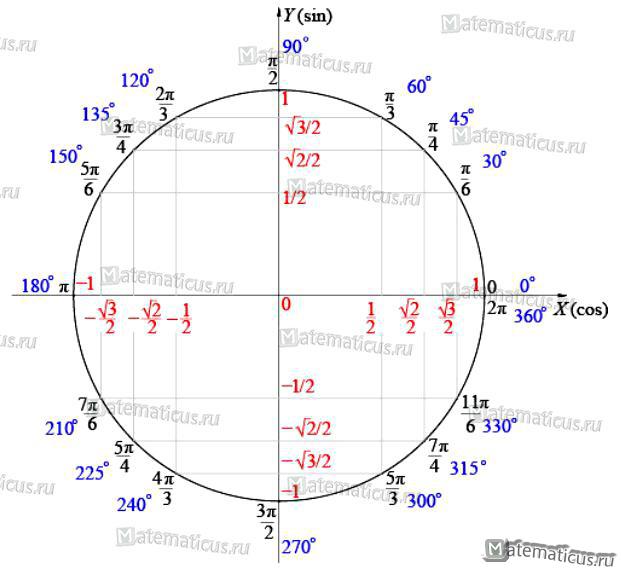
В этой статье мы поговорим об основах тригонометрии - о тригонометрической окружности. С нее начинается изучение тригонометрии в м классе. Именно тригонометрические уравнения, как правило, попадаются в самом легком задании второй части ЕГЭ по профильной математике. А умение преобразовывать тригонометрические выражения может пригодиться и в первой части. Без этой важной темы на ЕГЭ никак не обойтись.
